Maple 16/17: прорыв в скорости аналитических расчетов и моделировании

Интерфейс пользователя и справка Maple 16/17

Будучи системой компьютерной алгебры, Maple 17 имеет беспрецедентный по мощности аппарат реализации численных вычислений и графической визуализации [1]. Внешне интерфейс пользователя Maple 17 (рис. 1) заметно не изменился по сравнению с интерфейсом предшествующей версии Maple 16, появившейся всего годом ранее, но существенно отличается от интерфейса конкурирующей системы Mathematica 9. По обе стороны от рабочего окна (в центре рис. 1) расположены легко убираемые панели инструментов для объектов, указываемых в строках ввода. Строки вывода формируются автоматически и по желанию пользователя нумеруются. Сверху под титульной строкой расположена строка меню, снизу находится строка статуса.

Рис. 1. Окно интерфейса пользователя системы Maple 17

Внешне огромная справка системы со многими тысячами примеров предельно упрощена (рис. 2). Открывая с помощью гиперссылок те или иные разделы справки, можно убедиться в ее необъятности и простоте доступа к каждой команде и функции. Многие разделы справки содержат типовые примеры графической визуализации, маплеты (окна GUI), самоучители и ассистенты. В справке имеется огромное число демонстрационных примеров, предусмотрен их перенос в основное рабочее окно системы.

Рис. 2. Окно справки с началом раздела по новым возможностям Maple 17

Как и в системе Mathematica 9, в Maple 17 большое внимание уделено описанию в справке новых конкретных возможностей текущей версии системы (рис. 2, например). В частности, есть алфавитный и тематический каталоги новинок системы и наиболее важные ее разделы.

Работа с системой Maple 16/17

Работа с системой заключается в задании исходных выражений в строках ввода и получении результата вычислений в строках вывода после нажатия клавиши Enter. Двоеточие после выражения блокирует вывод результатов его вычислений, точка с запятой или отсутствие конечного символа позволяют получать результат вычислений. На рис. 3 изображено рабочее окно с примером на вычисление функции нормального распределения вероятностей с построением ее графика и гистограммы. Там же показано окошко с данными о системе Maple 17. Из него видно, что система выпущена 21 февраля 2013 года.

Рис. 3. Окно с примером вычисления функции нормального распределения вероятностей

При решении ряда задач рекомендуется решение каждой из них начать с очистки системы командой restart. Она, в частности, убирает определения всех переменных и освобождает память ПК от определенных функций и процедур. Все переменные становятся неопределенными и могут использоваться в символьных вычислениях.

Часть достаточно редко применяемых функций расположена в пакетах расширения системы. Для их применения нужные пакеты должны быть загружены командой with(name) или выбором из позиции Load Package в позиции Tools меню. Команду with без двоеточия используют и для получения списка функций данного пакета расширения. Например, для пакета логических операций имеем:

> with(Logic)
    [&and, &iff, &implies, &nand, &nor, &not, &or, &xor, BooleanSimplify, Canonicalize, Contradiction,
    Dual, Environment, Equivalent, Export, Implies, Import, Normalize, Random, Satisfy, TruthTable]

У большинства пакетов расширения (а их свыше 80) список функций куда более обширный. Все пакеты расширения указаны в разделе Packages справки.

Прорыв в скорости вычислений

В последние два-три года пользователи наблюдали огромные успехи команды фирмы Wolfram Research Inc. в совершенствовании системы компьютерной алгебры Mathematica. Вышли на рынок версии Mathematica 6, 7, 8 и 9. Каждая их них добавляла в ядро системы сотни новых команд и функций, а их время вычислений уменьшалось в десятки раз за счет улучшения алгоритмов и применения параллельных вычислений, возможных в современных ПК с многоядерными микропроцессорами.

Фирма Maplesoft — разработчик Maple развила «гонку версий» системы Maple с явным акцентом на совершенствование интерфейса пользователя и с меньшими успехами в обеспечении высокой производительности [2, 3]. Многим уже казалось, будто Mathematica обошла Maple и стала бесспорным лидером среди систем компьютерной алгебры. Однако за последний год положение явно изменилось в пользу Maple в связи с разработкой и выходом на рынок последних версий Maple 16 и 17.

Версия Maple 17 совершила прорыв в области ускорения вычислений даже в сравнении с предшествующей версией Maple 16. При этом в сотни раз уменьшено время вычисления элементарных математических функций, имеющих довольно сложные алгоритмы вычислений (рис. 4а).

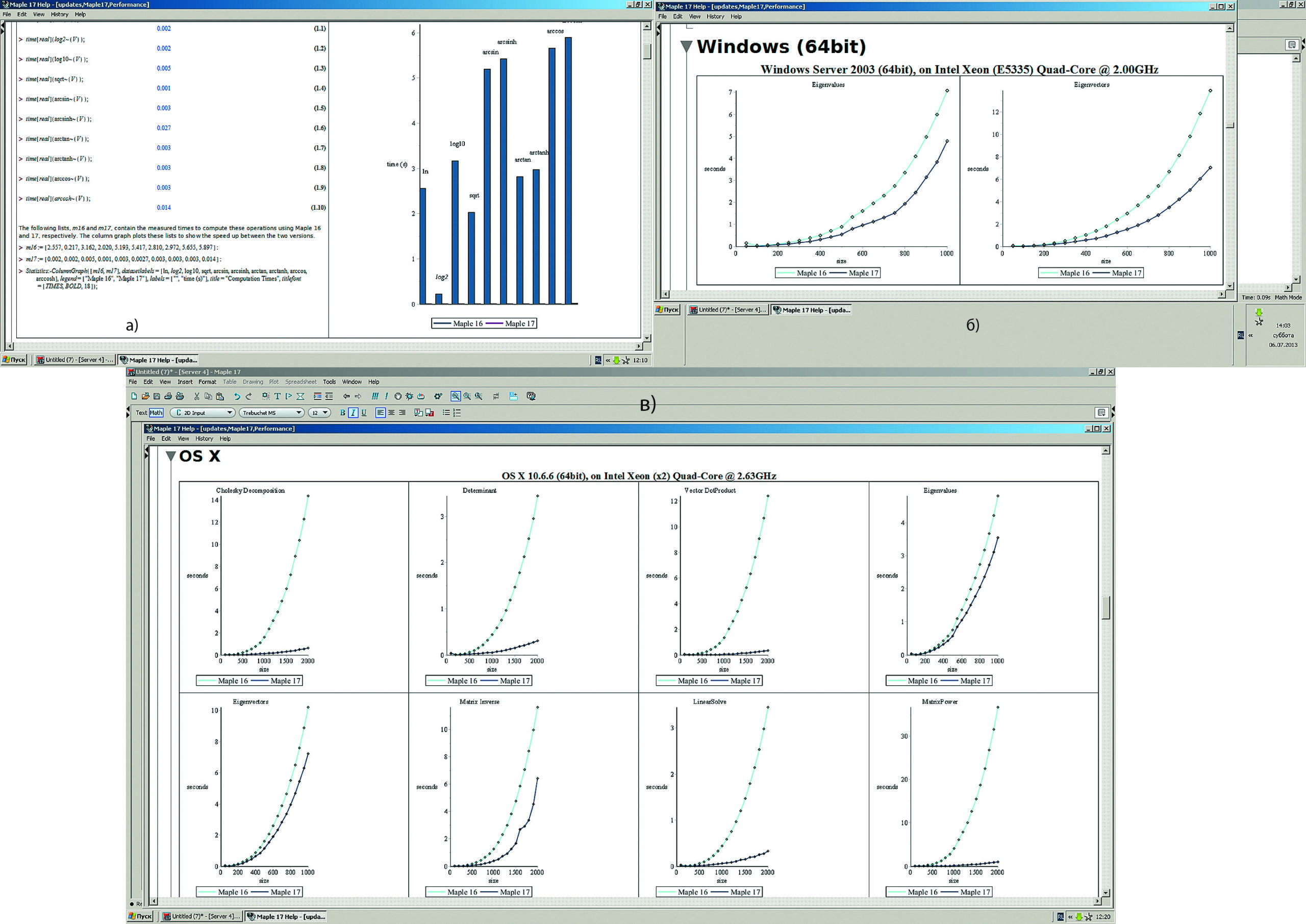
Рис. 4. Сравнение Maple 16 и Maple 17 по времени:
а) вычисления элементарных функций;
б) выполнения операций линейной алгебры при работе в операционной системе MAC OS;
в) выполнения операций вычисления собственных значений в операционной системе Windows 7

На рис. 4б показано сравнение Maple 16 и Maple 17 по времени выполнения операций линейной алгебры при работе в операционной системе MAC OS корпорации Apple. Здесь при больших размерах массивов разница не столь сенсационная, но, как правило, составляет не меньше десятка раз. Скорость вычисления собственных значений больших матриц иллюстрирует рис. 4в (64‑разрядная операционная система Windows 7).

Особенно поражает малое время вычислений при символьных (аналитических) вычислениях компьютерной алгебры. Чтобы избежать недоверия пользователя, разработчики Maple 17 пошли на беспрецедентный шаг — поместили в справку конкретные данные о времени выполнения различных аналитических вычислений в сравнении Maple 17 с предшествующей реализацией Maple 16 и даже новейшей Mathematica 9, выпущенной также в 2013 году. Применяемые для этого тестовые примеры даны на рис. 5.

Рис. 5. Шесть тестовых аналитических примеров (проблем)

На рис. 6а сравниваются системы Mathe-matica 9, Maple 16 и Maple 17 по скорости выполнения операции умножения для различных тестовых примеров. Для операции деления сложных выражений результаты приведены на рис. 6б. Выполнение функции factor над полученными ранее выражениями показано на рис. 6в.

Рис. 6. Сравнение Mathematica 9, Maple 16 и Maple 17 по скорости выполнения операции для различных тестовых примеров:
а) умножения;
б) деления;
в) функции factor

Факторизация более простых выражений показывает резкое уменьшение времени вычислений в системе Maple 17 (рис. 7а). Время выполнения операции расширения сложных выражений иллюстрирует рис. 7б. И здесь время вычислений в Maple 17 заметно меньше, чем у других систем.

Рис. 7. Время выполнения операции:
а) факторизации;
б) расширения Expand

Операции компьютерной алгебры и математического анализа

Операции компьютерной алгебры хорошо известны пользователям Maple и подробно описаны в книгах [2–4]. В Maple 17 они сохранены и расширены. Поэтому ограничимся несколькими примерами с применением функции упрощения simplify:

> restart;
> simplify(sin(x)^2+cos(x)^2,trig);
> e:=cos(x)^5+sin(x)^4+2*cos(x)^2–2*sin(x)^2–cos(2*x);

> simplify(e);

> simplify(GAMMA(n+4)/GAMMA(n),GAMMA);

> r:=RootOf(x^2–2=0,x):

> simplify(r^2,RootOf);

> simplify(1/r,RootOf);

> simplify(ln(x*y),power,symbolic);

При анализе сигналов часто используются функции интегральных преобразований, например Гильберта, Лапласа и Фурье. Maple обеспечивает получение таких функций для аналитических и численных расчетов [5]. В систему включено огромное число функций. Advisor функций обеспечивает легкое получение их свойств:

> FunctionAdvisor( definition, exp);

> FunctionAdvisor(definition, GAMMA(z));

> FunctionAdvisor(analytic_extension, GAMMA);

Многие функции имеют двойное назначение. Если их имя начинается с большой буквы, функции называют инертными — они выводят аргумент в обычной математической форме, но блокируют выдачу результатов вычислений. Обычные функции с именами, начинающимися с малой буквы, выдают результат вычислений. В строках ввода функции и команды могут записываться в текстовой или математической форме (например, с помощью палитр математических символов).

Примеры вычисления сумм, произведений, производной и интегралов:

> restart; sum(i/(i+1),i=0..n);

> restart; sum(–exp(–k),k);

> sum(k*a^k,k);

> sum(1/k!,k=0..infinity);

> restart; Product(k^2,k=1..5)=product(k^2,k=1..5);

> Product(k^2,k)=product(k^2,k);

> restart; Diff(sin(x)^2,x)=diff(sin(x)^2,x);

> restart; Int(1/sqrt(1–x^2),x=0..1)=int(1/sqrt(1–x^2),x=0..1);

> Int(exp(–t)/t^(1/3), t=0..infinity)=int(exp(–t)/t^(1/3), t=0..infinity);

> Int(Int(Int((x^2+y^2)*z,x=0..a),y=0..a),z=0..a);

Для пошагового вычисления интегралов имеется маплет с графическим интерфейсом пользователя (GUI) (рис. 8). Подобные маплеты в Maple 17 есть практически по всем основным средствам компьютерной алгебры и математического анализа. Имеется также возможность создавать маплеты самим пользователем.

Рис. 8. Маплет для реализации пошагового интегрирования разными методами

Вычисление фундаментальных пределов иллюстрируют примеры:

> Limit(sin(x)/x,x=0)=limit(sin(x)/x,x=0);

> Limit((1+x)^(1/x),x=0)=limit((1+x)^(1/x),x=0);

> Limit((1+1/x)^x,x=infinity)=limit((1+1/x)^x,x=infinity);

> Limit(ln(1+x)/x,x=0)=limit(ln(1+x)/x,x=0);

> Limit((exp(x)–1)/x,x=0)=limit((exp(x)–1)/x,x=0);

> Limit(((1+x)^a–1)/x,x=0)=limit(((1+x)^a–1)/x,x=0);

Следующие примеры показывают решение уравнений и системы из двух уравнений:

> fsolve(x^5–x,x,complex);

> solve(erf(x)=1/2,x);

> fsolve(erf(x)=1/2);

> restart;eq:=exp(–x)=x;sol:=fsolve(exp(–x)=x,x);

> restart;eq1:=a*x+b*y=e; eq2:=c*x+d*y=f;

> solve({eq1,eq2},{x,y});

Интерполяция, аппроксимация и регрессия

Для аппроксимации аналитических функций часто используется разложение в ряд Тейлора (или Маклорена, если разложение идет относительно точки с x=0). Обычно порядок ряда ограничивают 8–10, поскольку иначе погрешность аппроксимации резко возрастает. Maple, благодаря возможности проведения точных аналитических методов, такого ограничения не имеет, но при большом порядке ряда увеличивает время вычислений. Тут очень кстати оказывается высокая скорость вычислений у Maple 17. Пример проведения аппроксимации рядом Тейлора дан на рис. 9.

Рис. 9. Маплет для аппроксимации аналитической функции рядом Тейлора

В общем случае используется полиномиальная аппроксимация (рис. 10). Все сказанное о порядке ряда Тейлора справедливо и для аппроксимации полиномом. В данном случае применяется функция интерполяции interp. Число точек исходной функции синуса N=10, число верных цифр при вычислениях выбрано намеренно чуть меньшим — p=9, что позволяет наблюдать расходимость вычислений в конце интервала аппроксимации. Выбрав большее значение p, можно устранить расходимость вычислений.

Рис. 10. Полиномиальная аппроксимация аналитической функции

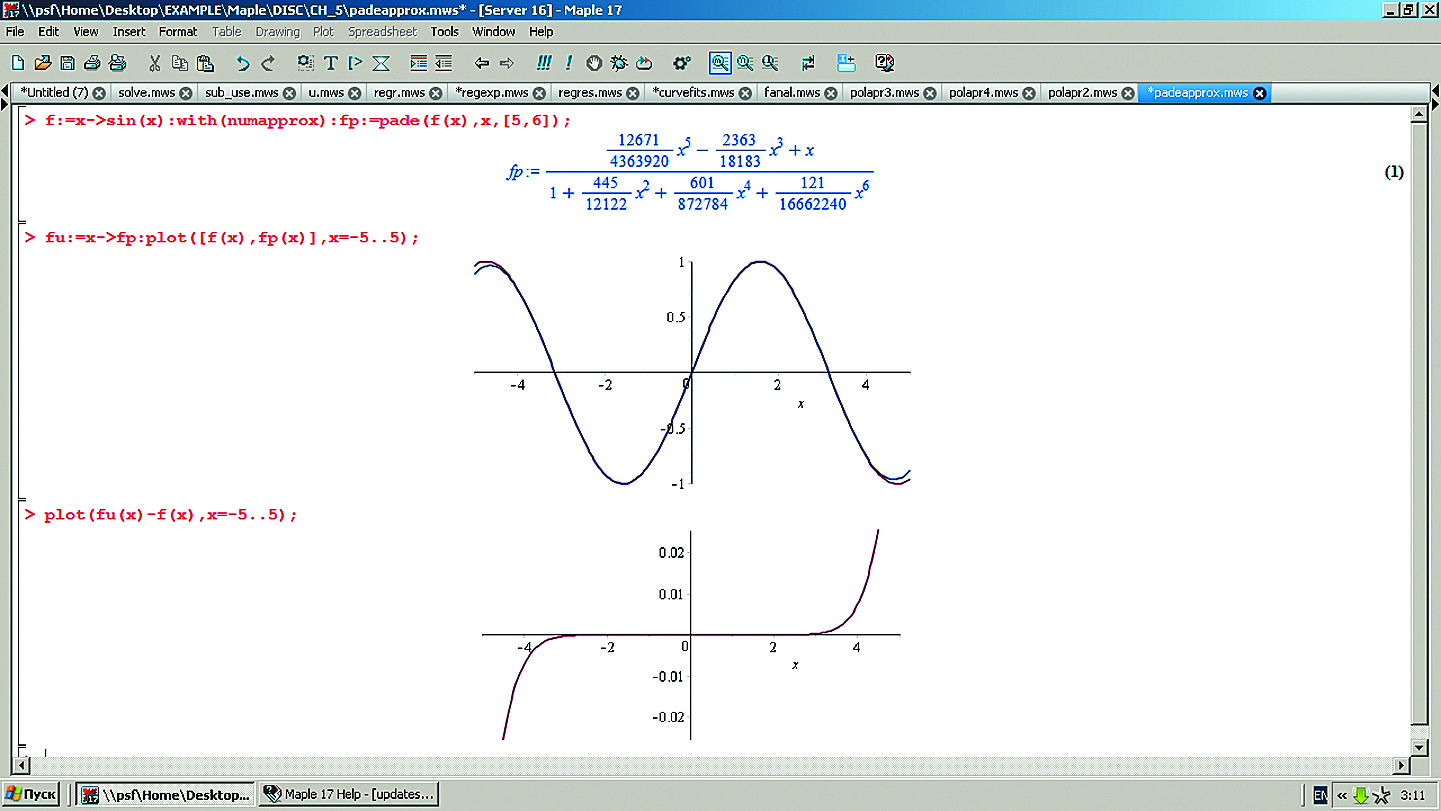
Большую точность и возможность аппроксимации функций с конечным числом нулей и полюсов обеспечивает аппроксимация Паде отношением двух полиномов. Пример такой аппроксимации функции синуса представлен на рис. 11.

Рис. 11. Аппроксимация Паде функции синуса

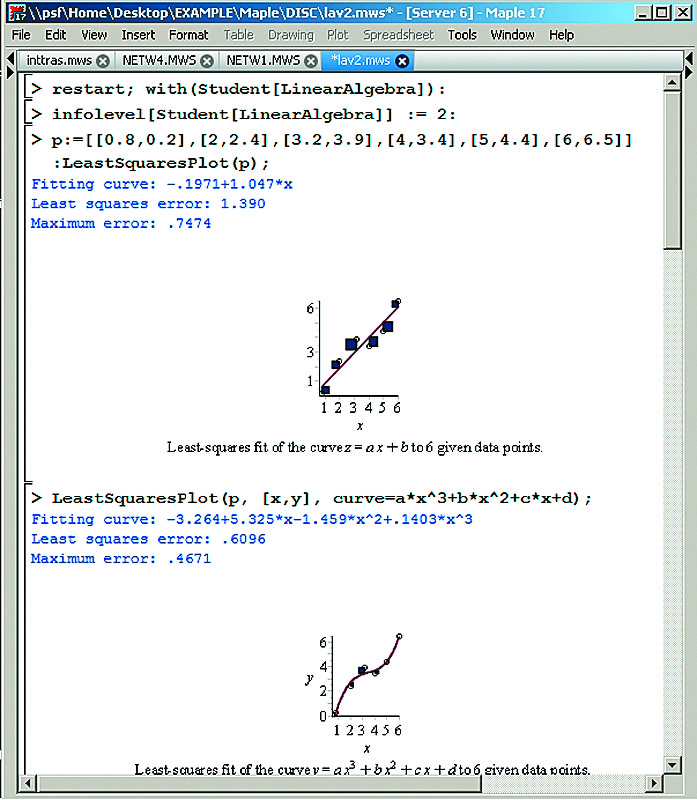
Поскольку точных исходных данных практически не бывает, специалисты-практики предпочитают точной аппроксимации регрессию с минимизацией ошибок отклонения исходных точек от линии регрессии по методу наименьших квадратов. На рис. 12 показано проведение линейной и нелинейной (полиномом третьей степени) регрессии с демонстрацией сути метода наименьших квадратов.

Рис. 12. Линейная и нелинейная регрессия (метод наименьших квадратов)

На рис. 13 приведено окно маплета по осуществлению интерполяции разными методами и регрессии по заданному выражению. Показано проведение линейной регрессии.

Рис. 13. Окно маплета по интерполяции и регрессии

Maple 17 способен решать практически любые задачи интерполяции, аппроксимации и регрессии, в том числе и для ряда переменных и многомерных массивов данных.

Графическая визуализация вычислений

В Maple 17 имеется около 400 графических команд, функций и опций, направленных на изменение типа и стиля графиков, цвета их компонентов, размера и местоположения и т. д. Эти средства используются в строках ввода, тогда как сами графики строятся в строках вывода. У многих функций есть возможность вращения изображения мышкой в любом направлении.

Обычно графики расположены в строках вывода по вертикали и имеют достаточно большой размер для удобного наблюдения (в Mathematica графики изначально выводятся маленькими). В строке вывода размещается один график. Но часто встречаются случаи, когда в окне нужно, например, разместить несколько задач с несколькими графиками (рис. 12). Maple имеет средства расположения нескольких графиков разного типа по горизонтали (рис. 14).

Рис. 14. Построение в одной строке вывода нескольких расположенных горизонтально графиков

Число отображаемых графиков настолько велико, что даже основную их часть нереально упомянуть в такой статье, как эта. По возможностям графики Maple 17 впору писать большую книгу в сотни страниц с цветными иллюстрациями высочайшего полиграфического качества. В России такая книга будет очень дорогой и уже в силу только этого недостаточно востребованной. А потому ограничимся лишь несколькими показательными примерами, которые легко позволяет воспроизвести превосходная полиграфическая база журнала «Компоненты и технологии». Подобная графика может быть основой 2D- и 3D-моделирования в архитектуре и механике.

Довольно распространенными являются графики с кривыми равного уровня — линиями пересечения трехмерных фигур параллельно расположенными плоскостями. Эти линии могут проектироваться на опорную плоскость или наноситься на исходную фигуру (поверхность) (рис. 15). Цветная закраска делает такие графики обычно наглядными и эстетичными.

Рис. 15. 2D- и 3D-графика с линиями равного уровня

В одном графическом окне можно строить несколько 3D-фигур или поверхностей, пересекающихся друг с другом (рис. 16). В этом случае Maple строит линии пересечения (с сохранением возможности построения линий равного уровня). На рис. 16 показано также открытое меню правой кнопки мыши, позволяющее использовать многочисленные команды редактирования уже созданного графика.

Рис. 16. Построение графика пересекающихся поверхностей

Разумеется, прежде всего вид графика определяется исходными математическими выражениями. Большие возможности открывает описание графиков параметрическими выражениями. О наглядности таких графиков свидетельствует рис. 17а, на котором представлено построение тора с «обмоткой» вокруг него. Это типичная математическая модель конструкции катушки индуктивности на тороидальном сердечнике. А на рис. 17б показано построение четырех скрученных спиралей. Там же представлено меню правой клавиши мышки для этого графика. Оно позволяет редактировать уже созданный график.

Рис. 17. Построение:
а) тора с обмоткой;
б) четырех закрученных трубчатых спиралей;
в) сложной фигуры с применением графических примитивов

Maple 17 имеет графические 2D- и 3D-при-митивы, начиная от отрезков прямых, дуг и окружностей и заканчивая сложными трехмерными объектами. Их совместное применение позволяет строить сложные графики на плоскости и в пространстве. Пример построения сложной 3D-фигуры показан на рис. 17в.

Решение дифференциальных уравнений

Решение дифференциальных уравнений и систем дифференциальных уравнений — важный и большой раздел математики. Maple всегда лидировала в средствах такого решения и его визуализации. Аналитические и численные методы решения дифференциальных уравнений годами оттачивались в многочисленных предшествующих версиях Maple, и весь этот мощный аппарат, естественно, вошел в новую реализацию Maple 17. Более того, фирма Maplesoft объявила, что в Maple 17 включено множество новых алгоритмов, команд, функций и опций для аналитического и численного решения систем дифференциальных уравнений, в том числе некоторых новых классов.

Для решения обыкновенных дифференциальных уравнений служит функция dsolve с большим набором опций. Приведем пример ее применения для аналитического решения одного дифференциального уравнения:

> dsolve(diff(y(x),x)–a*x=0,y(x));
> dsolve(diff(y(x),x)–y(x)=exp(–x),y(x));
> infolevel[dsolve] := 3:
> dsolve(diff(y(x),x)–y(x)=sin(x)*x,y(x));
Methods for first order ODEs:
--- Trying classification methods ---
trying a quadrature
trying 1st order linear
<- 1st order linear successful

В этом примере команда infosolve устанавливает уровень вывода решения.

Приведем примеры аналитического решения систем из двух дифференциальных уравнений (в том числе с заданием начальных условий):

> sys := diff(y(x),x)=2*z(x)–y(x)–x, diff(z(x),x)=y(x);fcns := {y(x), z(x)};
dsolve({sys,y(0)=0,z(0)=1},fcns);

> Order:=8:dsolve({sys,y(0)=0,z(0)=1},fcns,series);

> dsolve({sys,y(0)=0,z(0)=1},fcns,laplace);

В двух последних примерах решение представлено в виде степенного ряда, причем в последнем случае использовано преобразование Лапласа.

На рис. 18 показан пример решения дифференциального уравнения с построением асимптотических решений на фоне графика векторного поля. Векторное поле строится короткими стрелками, которые указывают на направление изменения поля. Подобное решение относится к сфере профессиональных методов решения дифференциальных уравнений. Для этого используется пакет расширения DEtools (и PDEtools для решения дифференциальных уравнений в частных производных).

Рис. 18. Пример асимптотического решения дифференциального уравнения

Математическое моделирование в аналитическом виде

Решение волнового дифференциального уравнения Бюргерса в частных производных для движения поначалу синусоидальной волны в нелинейной среде иллюстрирует рис. 19. Отчетливо видно, что со временем фронт волны обостряется, что находит применение в реальной технике генерации сверхкоротких импульсов [6]. Это связано с тем, что верхушка волны в нелинейной среде двигается быстрее, чем нижняя часть волны.

Рис. 19. Пример решения волнового уравнения Бюргерса в частных производных

Как известно, бомбардировка тонкой фольги α-частицами по фактам их отклонения позволила экспериментально открыть существование атомного ядра. Моделирование этого классического эксперимента в Maple 17 представлено на рис. 20.

Рис. 20. Вычисление траектории α-частицы

Здесь построены траектории движения α-частиц вблизи ядра (кружок с крестиком) (рис. 21). Видно не только отклонение, но и изменение направления движений (отражение частицы ядром без учета возможного эффекта поглощения такой частицы ядром).

Рис. 21. Траектории движения α-частиц вблизи ядра атома

Наличие аппарата преобразования аналитических выражений позволяет использовать технику таких преобразований для реализации аналитических методов расчета и моделирования, таких как интеграл Дюамеля и свертка, преобразование Лапласа, лежащее в основе операторного метода, и т. д. При этом решение удается получить в аналитическом виде и с его графической визуализацией.

На рис. 22а приведен пример аналитического моделирования последовательной LRC-цепочки при воздействии в виде экспоненциального перепада напряжения. Показано аналитическое решение задачи с применением интеграла Дюамеля и графики переходных процессов.

Рис. 22. Аналитическое моделирование последовательной LRC-цепочки при воздействии:
а) в виде экспоненциального перепада напряжения;
б) в виде затухающей синусоиды

Стоит изменить функцию, воздействия и можно смоделировать другой случай — поведения цепи при воздействии в виде затухающей синусоиды. Этот случай показан на рис. 22б. Обратите внимание на изменение вида выражения, описывающего решение.

Из этих примеров можно заметить недостаток аналитических методов моделирования — они для простых задач обычно получаются более громоздкими, чем привычные численные методы, зато дают решение в самом общем виде и без вычислительных погрешностей.

Пример проектирования цифрового полосового фильтра

Большие возможности Maple в обработке сигналов демонстрирует пример проектирования полосового цифрового фильтра с конечной импульсной характеристикой для выделения пятой гармоники сигнала. Исходные данные для фильтра задаются в начале проектирования (рис. 23а).

Рис. 23. Проектирование цифрового полосового фильтра:
а) окно 1;
б) окно 2;
в) окно 3;
г) окно 4;
д) окно 5

Это задание продолжено на рис. 23б, в конце которого строится импульсная характеристика фильтра. В конце данной части документа задан входной сигнал в виде меандра с частотой 500 Гц и размахом напряжения в 2 В.

Построение амплитудно-частотной характеристики (АЧХ) фильтра изображено на рис. 23в.

На рис. 23г представлен расчет временной зависимости входного сигнала и временной зависимости выходного сигнала (реакции). Из последней видно, что фильтр неплохо справляется с выделением пятой гармоники сигнала и имеет практически синусоидальный сигнал в стационарном режиме. Входной сигнал имеет довольно заметные шумы квантования, они видны и на выходном сигнале.

Спектральный анализ выходного сигнала фильтра и построение его спектра представлены на рис. 23д. Они подтверждают сделанное заключение о выделении пятой гармоники входного сигнала. На спектре отчетливо выделяется единственный пик с частотой 2500 Гц, стоящий на небольшом шумовом пьедестале.

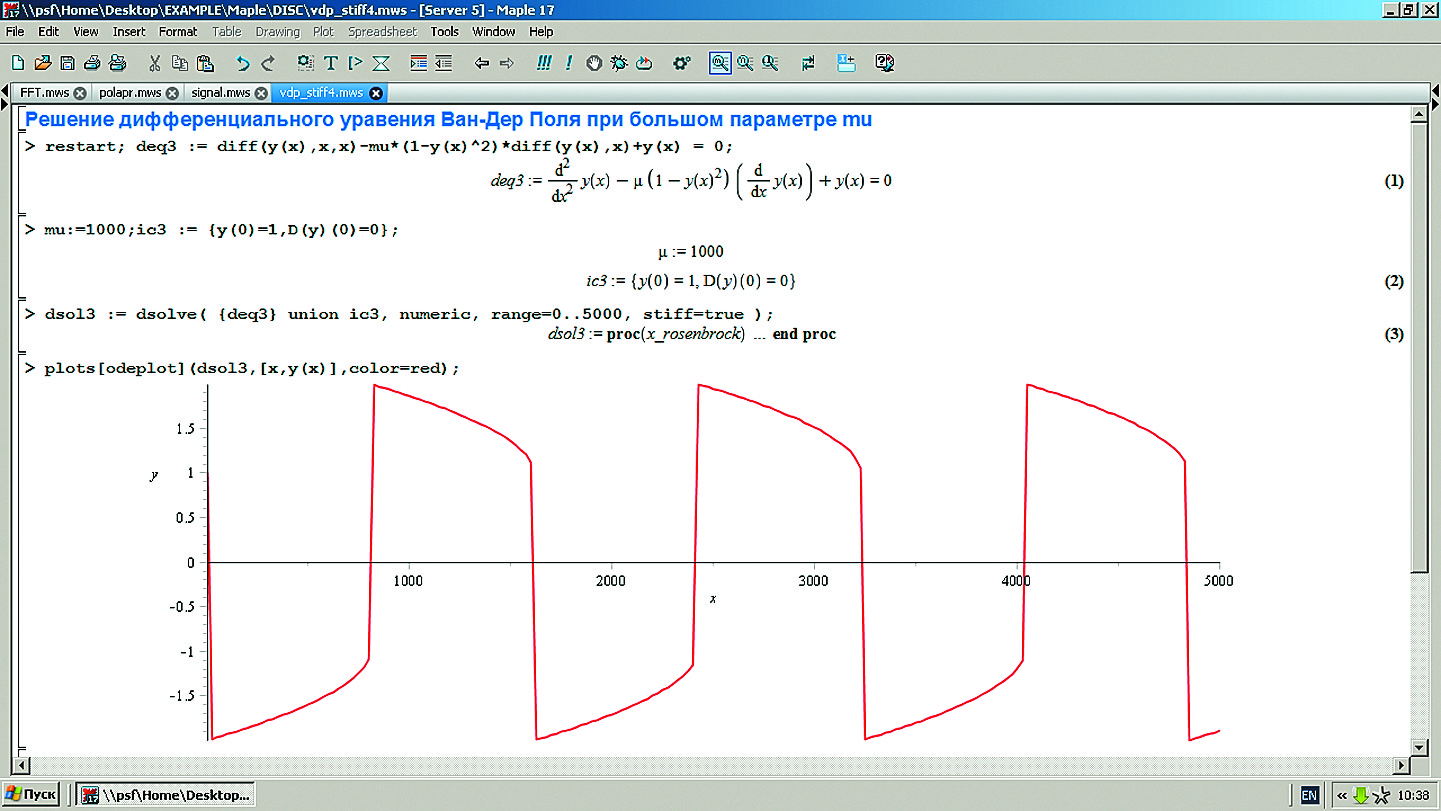
Решение жестких дифференциальных уравнений

Иногда, казалось бы, вполне правильно заданные дифференциальные уравнения или системы дифференциальных уравнений не решаются обычными численными методами. Часто такая ситуация возникает в случае жестких дифференциальных уравнений, в решении которых встречаются экспоненциальные члены с сильно различающимися постоянными времени и когда решение содержит участки, близкие к разрывным.

Для решения жестких дифференциальных уравнений и систем с такими уравнениями служат специальные решатели. Пример решения задачи, описываемой таким дифференциальным уравнением, показан на рис. 24.

Рис. 24. Моделирование колебательной системы Ван-дер-Поля при большом значении параметра μ

Маплеты и другие средства GUI

Некоторые примеры применения системы Maple носят настолько массовый характер, что для их реализации созданы специальные средства на основе графического интерфейса пользователя (Graphic User Interface — GUI). Такие средства в Maple названы маплетами (maplets). Они содержат окно с элементами интерактивного управления, панели ввода и вывода и другие средства. Примеры применения маплетов даны на рис. 8, 9 и 13.

Типичный маплет для изучения поведения последовательной LRС-цепи показан на рис. 25. При построении маплета используется имитационное моделирование цепи с помощью дифференциального уравнения второго порядка. Полное описание средств создания этого маплета дано в [2].

Рис. 25. Маплет анализа переходных процессов в последовательной LRC-цепи

В справке Maple 17 можно найти описание десятков типов маплетов для решения математических и физических задач — от построения простых графиков до решения сложных дифференциальных уравнений. Большинство из них выполнено на высоком профессиональном уровне (рис. 26). Хотя считать маплеты окончательно доработанными едва ли правильно.

Рис. 26. Окно GUI, имитирующее генератор сигналов

Эти средства широко применяются в:

• самоучителях (Tutors);
• ассистентах (Assistants);
• дополнительных примерах (Tasks).

Доступ к ним и пакетам расширения системы обеспечивает позиция Tools (инструменты) меню. В Maple 17 набор таких средств существенно увеличен.

Заключение

Новейшая система компьютерной алгебры Maple 17 обеспечила сенсационное уменьшение времени вычислений большинства математических операций, заметно обогнав конкурирующую систему компьютерной алгебры Mathematica 9. Число функций и команд в Maple 17 превысило пять с половиной тысяч! Многие сотни из них включены в ядро системы впервые. Maple 17 успешно осуществляет парадигму смешанных аналитических и численных вычислений и математического моделирования с высочайшим полиграфическим качеством их графической визуализации.